What Does 56 Download 7 Upload Mean

What does RMSE really mean?

Root Mean Square Error (RMSE) is a standard style to measure the error of a model in predicting quantitative information. Formally it is defined as follows:

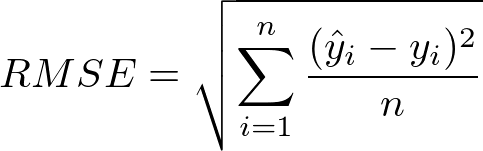
Permit's try to explore why this measure of error makes sense from a mathematical perspective. Ignoring the division by north under the square root, the commencement thing we can detect is a resemblance to the formula for the Euclidean altitude between ii vectors in ℝⁿ:

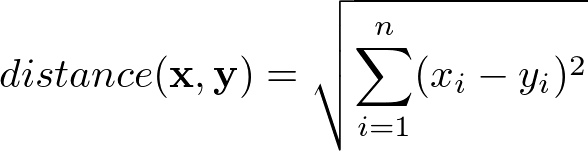
This tells united states of america heuristically that RMSE can be idea of equally some kind of (normalized) altitude between the vector of predicted values and the vector of observed values.

But why are we dividing by north under the square root here? If we continue n (the number of observations) fixed, all it does is rescale the Euclidean altitude by a factor of √(1/due north). It'due south a bit tricky to see why this is the correct thing to do, and so let's delve in a bit deeper.

Imagine that our observed values are determined by calculation random "errors" to each of the predicted values, equally follows:

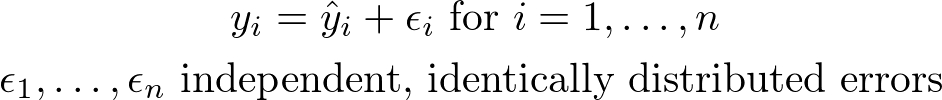
These errors, idea of as random variables, might have Gaussian distribution with mean μ and standard deviation σ, just whatever other distribution with a square-integrable PDF (probability density role) would also work. We desire to call back of ŷᵢ every bit an underlying physical quantity, such as the exact distance from Mars to the Sun at a particular signal in fourth dimension. Our observed quantity yᵢ would and then be the altitude from Mars to the Sun as we measure it, with some errors coming from mis-calibration of our telescopes and measurement dissonance from atmospheric interference.

Picture of the Sun and Mars — (NOT TO SCALE)

The hateful μ of the distribution of our errors would stand for to a persistent bias coming from mis-calibration, while the standard departure σ would correspond to the corporeality of measurement noise. Imagine at present that we know the mean μ of the distribution for our errors exactly and would like to approximate the standard deviation σ. We can see through a bit of calculation that:

Here E[…] is the expectation, and Var(…) is the variance. We can replace the average of the expectations E[εᵢ²] on the 3rd line with the E[ε²] on the quaternary line where ε is a variable with the same distribution as each of the εᵢ, because the errors εᵢ are identically distributed, and thus their squares all take the aforementioned expectation.

Remember that we assumed we already knew μ exactly. That is, the persistent bias in our instruments is a known bias, rather than an unknown bias. And so nosotros might as well correct for this bias right off the bat by subtracting μ from all our raw observations. That is, we might as well suppose our errors are already distributed with hateful μ = 0. Plugging this into the equation higher up and taking the square root of both sides then yields:

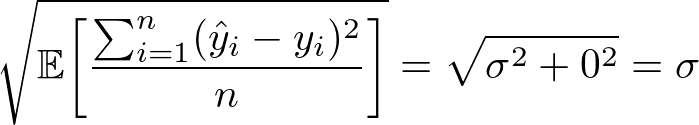
Notice the left paw side looks familiar! If we removed the expectation Eastward[ … ] from inside the square root, it is exactly our formula for RMSE class before. The central limit theorem tells u.s. that as north gets larger, the variance of the quantity Σᵢ (ŷᵢ — yᵢ)² / n = Σᵢ (εᵢ)² / northward should converge to zero. In fact a sharper form of the central limit theorem tell the states its variance should converge to 0 asymptotically like 1/north. This tells us that Σᵢ (ŷᵢ — yᵢ)² / n is a skilful computer for E[Σᵢ (ŷᵢ — yᵢ)² / n] = σ². But then RMSE is a good estimator for the standard deviation σ of the distribution of our errors!

We should also at present take an explanation for the segmentation by n under the square root in RMSE: information technology allows u.s. to gauge the standard deviation σ of the error for a typical single observation rather than some kind of "total error". By dividing by n, nosotros keep this measure of mistake consistent as we move from a small collection of observations to a larger collection (it just becomes more accurate as nosotros increase the number of observations). To phrase it another way, RMSE is a good fashion to answer the question: "How far off should nosotros expect our model to exist on its next prediction?"

To sum upward our give-and-take, RMSE is a practiced measure to use if we want to estimate the standard deviation σ of a typical observed value from our model's prediction, assuming that our observed data tin can exist decomposed as:

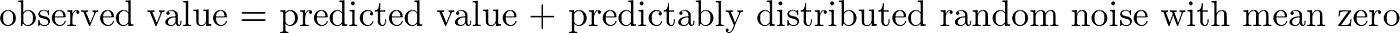
The random noise here could be anything that our model does not capture (e.g., unknown variables that might influence the observed values). If the dissonance is small, every bit estimated by RMSE, this mostly means our model is adept at predicting our observed data, and if RMSE is large, this generally means our model is failing to business relationship for of import features underlying our data.

RMSE in Data Scientific discipline: Subtleties of Using RMSE

In data science, RMSE has a double purpose:

To serve as a heuristic for preparation models
To evaluate trained models for usefulness / accurateness

This raises an of import question: What does it mean for RMSE to exist "small"?

Nosotros should notation first and foremost that "small" volition depend on our choice of units, and on the specific awarding we are hoping for. 100 inches is a big error in a building pattern, but 100 nanometers is not. On the other hand, 100 nanometers is a small error in fabricating an water ice cube tray, only mayhap a big error in fabricating an integrated circuit.

For training models, information technology doesn't really matter what units we are using, since all we care about during preparation is having a heuristic to help united states subtract the error with each iteration. We intendance only about relative size of the fault from one step to the next, not the absolute size of the error.

But in evaluating trained models in data science for usefulness / accurateness , we do intendance nigh units, because nosotros aren't simply trying to see if we're doing better than last time: we want to know if our model tin really help us solve a practical problem. The subtlety hither is that evaluating whether RMSE is sufficiently small or not will depend on how accurate nosotros need our model to be for our given application. In that location is never going to exist a mathematical formula for this, because it depends on things similar human intentions ("What are you lot intending to do with this model?"), risk aversion ("How much damage would be acquired be if this model fabricated a bad prediction?"), etc.

Besides units, there is another consideration besides: "small-scale" also needs to be measured relative to the type of model being used, the number of data points, and the history of training the model went through before you evaluated it for accuracy. At first this may audio counter-intuitive, but non when you lot remember the problem of over-fitting.

There is a adventure of over-plumbing fixtures whenever the number of parameters in your model is large relative to the number of data points y'all have. For example, if we are trying to predict one real quantity y every bit a function of another real quantity x, and our observations are (xᵢ, yᵢ) with 10₁ < x₂ < ten₃ … , a general interpolation theorem tells usa in that location is some polynomial f(ten) of degree at most northward+1 with f(xᵢ) = yᵢ for i = 1, … , n. This means if we chose our model to be a degree n+1 polynomial, by tweaking the parameters of our model (the coefficients of the polynomial), nosotros would be able to bring RMSE all the way downward to 0. This is truthful regardless of what our y values are. In this case RMSE isn't really telling u.s. anything nigh the accuracy of our underlying model: we were guaranteed to exist able to tweak parameters to go RMSE = 0 equally measured measured on our existing data points regardless of whether there is any relationship between the two real quantities at all.

But it'south non only when the number of parameters exceeds the number of data points that nosotros might run into issues. Even if nosotros don't have an absurdly excessive corporeality of parameters, it may exist that general mathematical principles together with mild groundwork assumptions on our data guarantee us with a high probability that by tweaking the parameters in our model, we can bring the RMSE below a certain threshold. If we are in such a situation, so RMSE beingness below this threshold may not say annihilation meaningful about our model's predictive ability.

If we wanted to call back like a statistician, the question we would be asking is not "Is the RMSE of our trained model small?" but rather, "What is the probability the RMSE of our trained model on such-and-such set of observations would exist this small by random chance?"

These kinds of questions get a bit complicated (you actually accept to do statistics), merely hopefully y'all get the picture show of why in that location is no predetermined threshold for "small enough RMSE", every bit easy as that would brand our lives.